Just how big is it?

[Qqmike]

Uh, well ... It's a matter of words, terminology.
0.99999.... = 1 in the sense that the left side converges to the right side; or even more precisely, the limit of the series represented by the left side is equal to "1." Limit, as in mathematical limit, as in arbitrarily close, as in "choose any arbitrary epsilon positive," and you can show that a member of the series on the left is within epsilon of the right. And so on. I know what you guys mean to say, colloquially, but I'm not sure you know what I'm trying to say. I am making precise what you mean to say! The left is not equal to the right but only in the sense that the infinite series represented by the left converges in the real number field to the number 1. There, that's better.
http://en.wikipedia.org/wiki/Limit_%28mathematics%29
I'm not picking at straws, I'm, just trying to be precise.
If, for example, you focus ONLY on the ring of positive integers embedded in the real field, then what?! There is not such thing as 0.9999...., and so then what is "1"? (1, viewed "as itself," as a positive integer, etc.)

[HalationEffect]

"they are the same number. " -- Well, only in the sense that the infinite series of summations of negative powers of ten CONVERGES to 1 (i.e., 1 is the limit of the series), using the real number system as a "field." But, of course, in a number theoretic sense, or set theoretic sense, or ring theoretic sense, for example, the number "1" (so-called) is another animal. Right?

Just follow the link Snowhog posted to see that there are several formal mathematical proofs that they're the same number.

[Snowhog]

0.999...

In mathematics, the repeating decimal0.999... (sometimes written with more or fewer 9s before the final ellipsis, or as 0.9, 0.(9), or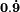 ) denotes a real number that can be shown to be the number one. In other words, the symbols "0.999..." and "1" represent the same number. Proofs of this equality have been formulated with varying degrees of mathematical rigor, taking into account preferred development of the real numbers, background assumptions, historical context, and target audience.Every nonzero, terminating decimal has an equal twin representation with trailing 9s, such as 8.32 and 8.31999... The terminating decimal representation is almost always preferred, contributing to the misconception that it is the only representation. The same phenomenon occurs in all other bases or in any similar representation of the real numbers.
The equality of 0.999... and 1 is closely related to the absence of nonzero infinitesimals in the real number system, the most commonly used system in mathematical analysis. Some alternative number systems, such as the hyperreals, do contain nonzero infinitesimals. In most such number systems, the standard interpretation of the expression 0.999... makes it equal to 1, but in some of these number systems, the symbol "0.999..." admits other interpretations that contain infinitely many 9s while falling infinitesimally short of 1.
The equality 0.999... = 1 has long been accepted by mathematicians and is part of general mathematical education. Nonetheless, some students find it sufficiently counterintuitive that they question or reject it, commonly enough that the difficulty of convincing them of the validity of this identity has been the subject of numerous studies in mathematics education.

[Qqmike]

"they are the same number. " -- Well, only in the sense that the infinite series of summations of negative powers of ten CONVERGES to 1 (i.e., 1 is the limit of the series), using the real number system as a "field." But, of course, in a number theoretic sense, or set theoretic sense, or ring theoretic sense, for example, the number "1" (so-called) is another animal. Right?

[HalationEffect]

More fun with numbers: 0.999... = 1. (Zero point nine nine nine recurring equals one).

Not just practically the same, or so close as makes no difference; they are the same number. Getting to grips with that idea really curdled my grey matter for a while!

[Detonate]

Yes, I have seen folks ponder on this question for hours without coming up with the correct answer when it is a simple Distance, Time, Rate problem. He must complete the two laps in two minutes to average 60 mph. He already used the two minutes on the first lap.

[HalationEffect]

Reminds me of the old trick math question.

I car goes around a circular one mile track, on the first lap the driver averages 30 MPH. How fast will he have to drive the second lap to average 60 mph for both laps?

Somewhat counter-intuitively, he'd have to go infinitely fast on that 2nd lap in order to average 60MPH over the two laps. Or, to put it another way, he'd have to complete the 2nd lap in zero time.

My favourite example of counter-intuitive mathematics is the Monty Hall problem.

[Detonate]

Reminds me of the old trick math question.

I car goes around a circular one mile track, on the first lap the driver averages 30 MPH. How fast will he have to drive the second lap to average 60 mph for both laps?

[woodsmoke]

Or like Chum, you can give out Secret Santa names and only have yours in the bag.

woodsmoke

[kubicle]

Not if you're a computer programmer, familiar with the approximation 2^10 ≈ 10^3, so 2^100 ≈ 10^30. You're given 500 sheets = 50 mm, so 1000 = 100 mm, so 10^4 = 1 m, thus the pile is 10^26 m. A lot. A light year ≈ 10^16 m, our galaxy 100,000 ly, so my answer was about 10^5 times the size of the Milky Way (5 being 26 - 16 - 5).

Regards, John Little

So you went for the easier way. I OTOH, will need one-hell-of-a paper cutter after just a few more cuts. Chuck Norris has already cut 200 times (with his bare hands of death).

[SteveRiley]

You were probably that kid who licked the candy he received at Christmas.

And everybody else's when they weren't looking.

[oshunluvr]

and Steve does that while announcing "hey, did anywad wunt dis las piece of pie?" through the first fork full.

You were probably that kid who licked the candy he received at Christmas.

[SteveRiley]

Reminds me of the last piece of pie or cake. No one wants to take the last peace so you cut it in half and take half.

Not me. I see that last piece and I scarf that sucker up.

[Snowhog]

hehe. I did say "theoretically", but maybe I should have said "philosophically".

Zeno's paradoxes

[jlittle]

And theoretically, if you stand at x distance from a wall, and walk only half the distance towards it, stopping, then again walking half the distance, theoretically, you'll never reach the wall!

That depends how long you stop for each time. If the time you pause tends towards zero as fast as the distance you walk, your extrapolation to "never" is invalid. Also, the uncertainty principle will apply pretty soon, too.

Regards, John the party pooper Little